Distances are a foundational concept in geometry. It concerns the separation of two points in space, and we usually consider these points to have no expanse themselves. Let's begin with a few basic facts about distances.
We will denote the distance between points \(P, Q\) as \(d(P, Q)\)
For any points \(P, Q\) we have \(d(P, Q) \geq 0\). \(d(P, Q) = 0\) if and only if \(P = Q\).
For any points \(P, Q\) we have \(d(P, Q) = d(Q, P)\)
For points \(P, Q, M\) we have \(d(P, M) \leq d(P, Q) + d(Q, M)\)
Expanding on the last one a little, we can introduce the concept of a segment. A segment can be thought of as the straight line connecting any two points. Therefore, if \(Q\) sits on the segment between \(P\) and \(M\) i.e. it is somewhere in between them, then \(d(P, M) = d(P, Q) + d(Q, M)\)
We can now think about some shapes. The simplest shape is perhaps the circle. For point \(P\) the circle is a line where every point on the line is distance \(r\) from \(P\). \(r\) is often called the radius.
As a quick remark here, in order to talk about distances we need some kind of measurement system. In the real world, this will usually be something like metres. In geometry, the neat thing is that absolute distances often don't matter much but the ratios between them. It's common to see one distance defined as "unit one", which can be taken to have length 1, with arbitrary distance units as such.
We can now define one of the most important concepts in geometry - the angle. An angle forms when two lines meet. Angles are usually measured in degrees. If two lines make a perfectly square cross that is a \(90^{\circ}\) angle. Four \(90^{\circ}\) angles make up a full circle, or \(360^{\circ}\).
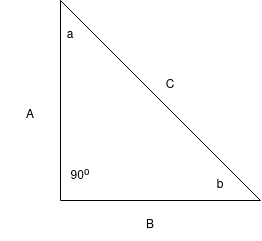
The favourite shape of most mathematicians though is the triangle. A triangle is a three sided shape. The sum of the internal angles where the three lines meet is always \(180^\circ\). To begin with, we will look at a particular subclass of triangles called right-angled triangles. These are triangles which have one of their angles be \(90^\circ).
In this triangle, the two other internal angles are each \(45^\circ\) since \(45^\circ + 45^\circ + 90^\circ = 180^\circ\).
In this triangle, sides \(A\) and \(B\) are the same length. Let's call them length 1. What is the length of side \(C\)? This introduces the most important formula in all of geometry - the Pythagorean theorem
\[A^2 + B^2 = C^2\]
Where \(C\) is always referring to the hypotenuse of a right angle triangle. The hypotenuse is the longest side (which is also never the side that helps form the right-angle itself). Please burn this formula into your memory - it will be one of the most used formulas going forward.
So, using this formula to find the length of \(C\) is quite easy
\[\sqrt{1^2 + 1^2} = C = \sqrt{2}\]