The unit of degrees is quite unnatural. All we are really doing there is taking a circle and arbitrarily splitting it into 360 equal segments. That number is arbitrary (although 360 has many factors so it is a convenient choice). There is another system called gradians which has 400 degrees in a full circle. You could in principle make any measurement system like this and choose any number of degrees
What about something more natural or self defining though? We introduce the radian, a unit of measure which is defined by \(\pi\). A right angle is \(\pi / 2\) radians. A half circle is \(\pi\) radians. A full circle is \(2\pi\) radians.
We define two functions relative to circles. The first is \(\sin(x)\) and the second is \(\cos(x)\).
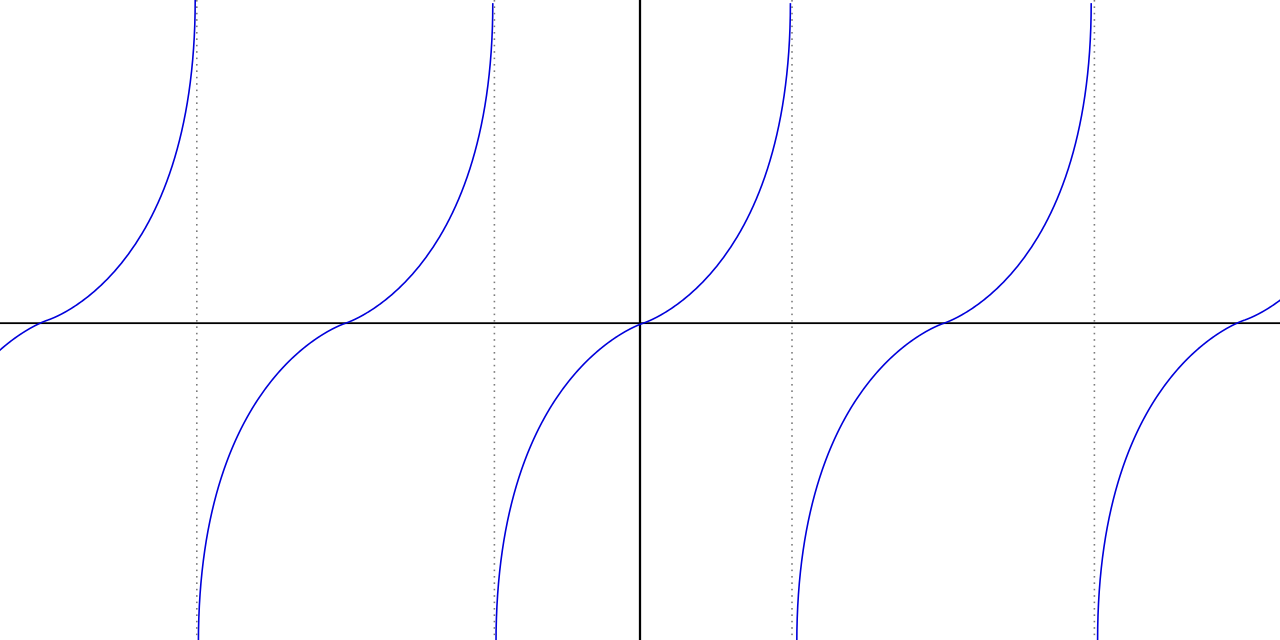
These graphs are actually just shifted with respect to one another. We can define a third function \(\tan(x) = \frac{\sin(x)}{\cos(x)}\). For the graph of this I will use a static image. That's just because \(\tan(x)\) has some asymptotes that go to infinity - which computers don't deal well with!
There are many beautiful properties of trigonometry, but for this introductory course we will simply be looking at how we can use these to help solve for the lengths and angles of right angle triangles.
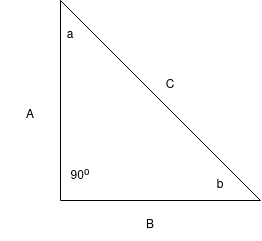
Let's try and work out the angles in the above example triangle. Try and burn the mnemonic SOHCAHTOA into your memory - it will help you memorise the important set of equations below
\[\sin(x) = \frac{\text{opposite}}{\text{hypotenuse}}\]
\[\cos(x) = \frac{\text{adjacent}}{\text{hypotenuse}}\]
\[\tan(x) = \frac{\text{opposite}}{\text{adjacent}}\]
So, looking at angle \(a\), The hypotenuse is line \(C\). The opposite of angle \(a\) is line \(B\). The adjacent to angle \(a\) is line \(A\). Always work out the hypotenuse first - technically two lines are "adjacent" to each angle as such, but only one of them will be the hypotenuse - the other must be the adjacent line!
I will use \(\sin(x)\) to work out this angle. We know the lengths of the hypotenuse and opposite so we can simply plug this in.
\[\sin(a) = \frac{1}{\sqrt{2}}\]
\[a = \sin^{-1}(\frac{1}{\sqrt{2}}) = 45^\circ\]
What is that \(\sin^{-1}\)? That is the inverse \(\sin\) function. There is an inverse function for each of the trig identities i.e. \(\cos^{-1}\), \(\tan^{-1}\). Sometimes these are called asin, acos anf atan, or even sometimes arcsin, arccos, arctan. All of them mean the same thing. The graphs of these inverse functions are below.
Have a go at finding all the lengths and angles in the following triangles yourself (tip: make sure your calculator is set to degrees! Also, the little square in the corner of these triangles means right angle. These triangles are not necessarily to scale so don't try and measure them!).
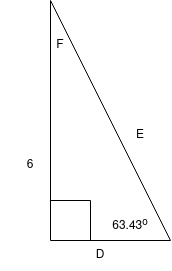
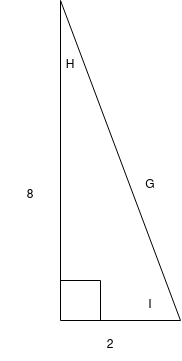
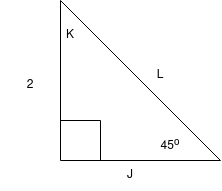
Answers
- \(D = 3\),\(E = 3 \sqrt{5} \approx 6.7\),\(F = 26.57^\circ\)
- \(G = 2\sqrt{12} \approx 8.24\),\(H = 14.04^\circ\),\(I = 75.96^\circ\)
- \(J = 2\),\(K = 45^\circ\),\(L = 2 \sqrt{2} \approx 2.82\)