Circuits have become an integral part of the modern world. From simple lightbulbs in every home, to complex computers, to specialised measurement equipment that makes science possible, it's clear that the modern world relies on circuits. Let's understand them!
What exactly is current in a wire? It is the flow of electrons in that wire. However, for historical reasons (mostly to keep the sign positive) current flows in the opposite direction to the direction the electrons actually flow. That isn't strictly important though for understanding the more fundamental concept. When we apply a field to a wire it applies a force to the electrons. If they are free to move, they will do so. Strictly speaking, these electrons were already moving, bounding around at incredible speeds. However, they will now have a net velocity in a particular direction. Since this is an average, we call it a drift velocity.
A metal wire of cross sectional area \(A\) contains \(n\) free electrons per cubic metre. If all of these electrons move along this wire in the same direction at speed \(u\), and each one has charge \(q\). We can work out the current by considering a thin slice of the wire and how many electrons pass through that per second. The current is therefore given by \(I = uneq\).
Let's suppose that a cable with a 13A current, with cross sectional area \(1.5mm^2\) and \(1.0 \times 10^{29}\) free electrons per cubic metre. We can use the above equation to find the drift velocity like so: \(u = \frac{I}{neq} = \frac{13}{1 \times 10^{29} \cdot 1.6 \times 10^{-19} \cdot 1.6 \times 10^{-6}} = 0.00054 \frac{m}{s}\). Are you surprised at how slow this is?
Let's do that again, now for a wire with a \(0.1 \times 0.2 mm\) cross section with \(10^{20}\) free electrons per cubic metre and a current of only 10mA. \(u = \frac{10 \times 10^{-3}}{10^20 \times 2 \times 10^{-8} \times 1.6 \times 10^{-19}} = 31250 \frac{m}{s}\). Are you surprised at how fast this is?
So, what exactly is carried around the wire? Sure, the electrons move , but we aren't actually interested in circuits for the electrons, we are interested in them for carrying energy (and thus information). Where is the energy? The electrons carry a very very tiny amount of kinetic energy. Let's look at this kinetic energy for the two wires we considered. A simple \(\frac{1}{2}mu^2\) is all we need. For the first wire \(\frac{1}{2} 9.109 \times 10^{-31} * 0.00054^2 = 1.32809 \times 10^{-37}\) joules per electron, or \(1.328 \times 10^{-8}\) joules per cubic metre. Remember, a cubic metre is a lot of cable. For the other wire it works out to around \(0.044\) joules per cubic metre. Maybe a little more, but still totally negligible. Just think about how big a cubic metre is. You probably don't even have a cubic metre of wire in your home. This clearly isn't the energy that keeps lights on and heats ovens. Strictly speaking the energy is in the field that is applied to the wire that causes the electrons to move. The field will be generated by some process: maybe a chemical process (like in a battery) or motion (like the rotating turbine in a steam power plant).
Many materials follow Ohm's law - which states that
\[R = \frac{V}{I}\]
where \(R\) is the resistance, \(V\) is the voltage and \(I\) is the current. We have already covered current - physically, this is the flow of electrons themselves. Voltage is the field we have talked about - another term for voltage is "potential difference". Strictly, there is no "absolute" measure of voltage, only a voltage difference between two points. This is analogous to the potential different in a falling under gravity problem. When an object is high in the air, it has a larger potential and so falls to a place it will have a lower potential. The analogy breaks down a little since, as we discussed, very little actually gets converted into kinetic energy with electricity. Resistance in an electrical circuit is analogous to the air in falling under gravity problems. The big different here is that in kinematics problems we usually ignore air resistance since it is very very tiny. We can not ignore it here though as it is very significant. This makes intuitive sense - you can run through air but if you ran full speed into a steel wall you'd have very little chance of making it through!
Some materials do not follow Ohm's law, but the resistance becomes a function of the current
\[R(I) = \frac{V}{I}\]
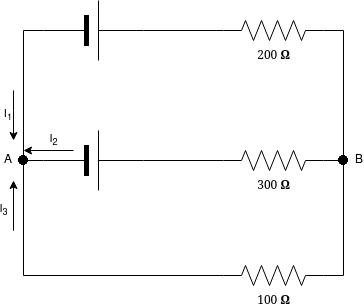
Take a look at the above circuit. We want to Work out the potential difference between point A and B. In order to do this we use Kirchoff's laws. There are two relevant laws at play here. The first is that for any point, the current flowing in and the current flowing out must be the same. That's what these arrows around point A indicate. They all point in on the diagram - this doesn't matter, the ones that are flowing out will simply come out negative. The other law is that whichever route we take between two points, the voltage will always be the same. Therefore, we get
\[I_1 + I_2 + I_3 = 0\]
\[V = 3 - 200 I_1\]
\[V = 4 - 300 I_2\]
\[V = -100 I_3\]
We have four unknowns and four equations. Try and solve these simultaneous equations yourself: verify that \(V \approx 1.55 V\).
So far we've looked at direct current. We can now look at alternating current. Alternating current is a little more tricky but much more useful - the plugs in your home are an alternating current source. Consider something that generates a field - a potential difference - and does so according to some sin relationship
\[V = \Re V_0 e^{i \omega t}\]
Then the current will also vary with the voltage
\[I = \Re I_0 e^{i \phi} e^{i \omega t}\]
The introduction of \(\phi\) into the current term should hopefully tip you off that they may not necessarily be in step with one another.
With simple direct current circuits the power is given by
\[P = IV\]
However, in an alternating current circuit, since the current will not be steady, then neither will the power. Instead it will be given by
\[P = VI = V_0 \cos(\omega t) I_0 \cos(\omega t) = V_0 I_0 \cos^2(\omega t)\]
assuming no phase offset (like in a resistor). The average power is then
\[\bar{P} = \frac{1}{2} V_0 I_0\]
To clean up that factor of one half, we introduce the concept of the root mean squared value or rms. \(V_{rms} = \frac{1}{\sqrt{2}}V_0\) and \(I_{rms} = \frac{1}{\sqrt{2}}I_0\). Thus
\[\bar{P} = V_{rms} I_{rms}\]