Let's define a new concept: momentum. The momentum of an object is equal to its mass times its velocity, as an equation this is
\[\mathbf{p} = m \mathbf{v}\]
Notice how momentum and velocity are vectors.
Making another definition, a famous one from Newton, we define the force as the rate of change of momentum
\[\mathbf{F} = \frac{d}{dt} \mathbf{p}\]
We can clearly see then that a body can only have a change in momentum if a force is applied. Imagine a body floating in space. With no friction, gravity or other forces it will continue at that velocity forever. Therefore, we say its state of motion is constant. When a force is applied, its momentum will by definition change - by definition changing its velocity. Imagine our body floated near a planet which applied a gravitational force, it would change direction. Therefore, its momentum and velocity has changed.
Imagine three objects moving around in some space. They are able to interact with each other, but do not interact with anything outside of themselves. Therefore, we have
\[\mathbf{p}_1 = m_1 \mathbf{v}_1, \mathbf{p}_2 = m_2 \mathbf{v}_2, \mathbf{p}_3 = m_3 \mathbf{v}_3\]
Consider object 1. Any changes in momentum it experiences are due to object 2 and object 3. Therefore
\[\frac{d}{dt} \mathbf{p}_1 = \mathbf{F}_{12} + \mathbf{F}_{13}\]
I use \(\mathbf{F}_{ij}\) to represent the force on \(i\) by \(j\)
We can make similar expressions for object 2 and object 3
\[\frac{d}{dt} \mathbf{p}_2 = \mathbf{F}_{21} + \mathbf{F}_{23}\]
\[\frac{d}{dt} \mathbf{p}_3 = \mathbf{F}_{31} + \mathbf{F}_{32}\]
Since the system as a whole is not interacting, all of these forces must sum to 0
\[\mathbf{F}_{12} + \mathbf{F}_{13} + \mathbf{F}_{21} + \mathbf{F}_{23} + \mathbf{F}_{31} + \mathbf{F}_{32} = 0\]
Therefore,
\[\frac{d}{dt} (\mathbf{p}_1 + \mathbf{p}_2 + \mathbf{p}_3) = 0
Integrating 0 means we have some constant value, therefore
\[\mathbf{p}_1 + \mathbf{p}_2 + \mathbf{p}_3 = \mathbf{P}\]
Where \(\mathbf{P}\) is some constant momentum of the system.
For a closed system, the total momentum is always constant!
This is one of the most important concepts in physics, so commit this to memory!
Let's try an example problem
a 10kg block is travelling at 5m/s and a 5kg block is travelling at 3m/s in the same direction. They collide and stick together. What is the velocity of the object after the collision?
Start by calculating total momentum before collision
\[10kg \times 5m/s + 5kg \times 3m/s = 65kg m/s\]
Since \(\mathbf{p} = m \mathbf{v}\)
\[15kg \times x = 65kg m/s\]
\[x = \frac{65kg m/s}{15kg} = 4.33 m/s\]
Now, we can define another property: impulse. Impulse is defined as force acting over a time. This would look like
\[\mathbf{I} = \int_0^t \mathbf{F} dt^\prime\]
In the much simpler case of a constant force, the impulse becomes
\[\mathbf{I} = \mathbf{F} \Delta t\]
Another way to express this is
\[\mathbf{I} = \int_0^t \mathbf{F} dt^\prime = \int_0^t \frac{d}{dt^\prime} \mathbf{p} dt^\prime = \mathbf{p}(t) - \mathbf{p}(0)\]
Let's try an impulse problem
A sandbag weighing 10kg is dropped from a hot air balloon which is travelling with a constant upward velocity of 10m/s from 600m. It hits the ground without bouncing. What is the impulse?
First, we need the velocity just before hitting the ground. For that, we need the time. We can use our familiar SUVAT equations to help us here. Using \(s = ut + \frac{1}{2}at^2\) we can solve for the time
\[-600 = 10t + \frac{1}{2} \times -9.81 t^2\]
Let me explain these numbers a little. I define the ground as 0m, and up as the positive direction. This means our sandbag will actually travel -600m, or 600m down.
\[-4.905t^2 + 10t + 600 = 0\]
We can use the quadratic formula to solve this
\[t = \frac{-10 \pm \sqrt{10^2 - 4 \times -4.905 \times 600}}{-9.81} = 12.126 or -10.088\]
Since we are not interested in solutions in the past, we ignore the negative time solution. Therefore, \(t = 12.126s\).
Using another SUVAT equation will let us solve for the velocity, \(v = u + at\)
\[v = 10 + -9.81 \times 12.126 = -108.95606 m/s^2\]
The impulse is equal to the momentum after some event minus the momentum before some event. The momentum of the sandbag just before hitting the ground is \(-108.95606 \times 10 = -1089.5606 kg m/s^2\). Therefore, the impulse is
\[I = 0 - -1089.5606 = 1089.5606kg m/s^2\]
Summary
\[\mathbf{p} = m \mathbf{v}\]
\[\mathbf{I} = \int_0^t \mathbf{F} dt^\prime = \int_0^t \frac{d}{dt^\prime} \mathbf{p} dt^\prime = \mathbf{p}(t) - \mathbf{p}(0)\]
Friction
Consider an object at rest on a table. Since there is no motion, we can deduce that the sum of forces in this system is 0. What does this mean practically? The table must be applying a force on the object! We call this a normal reaction force, and it will be equal to the weight of the object, in this case.
Now imagine this object starts to slide. Up till now we have ignored the force called friction, but let's start to consider it. Friction will act to oppose the direction of motion, and be some function of the normal force.
\[F = \mu_s N\]
Where \(F\) is the maximum static friction force, \(\mu_s\) is the static coefficient of friction and \(N\) is the normal force. When the object is moving though, there is a different (usually lower) coefficient of friction \(\mu_k\).
Consider a pulley on the edge of a table. It connects a 2kg weight on the table to a 5kg weight handing freely. What would the coefficient of friction have to be for the system to just remain static? Assume the pulley and ropes are smooth and light.
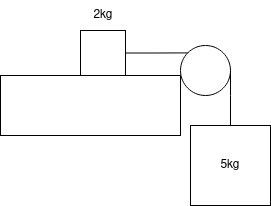
Solution
For the system to just remain static, the two blocks need to not be moving and the frictional force must be maximal.
In order for the 5kg block to not move, the tension in the rope must be equal to its weight
\[T = 5g\]
In order for the 2kg block to move move horizontally, the tension in the rope must equal the frictional force.
\[T = F_f\]
In order for the 2kg block to not move vertically, the normal force must be equal to its weight
\[N = 2g\]
And finally, a maximal friction means that
\[F_f = \mu_s N\]
Putting all of these together...
\[F_f = \mu_s N = 5g\]
\[2g \mu_s = 5g\]
\[\mu_s = \frac{5}{2}\]
Consider now a system where the blocks have two pulleys, as shown in the below diagram.
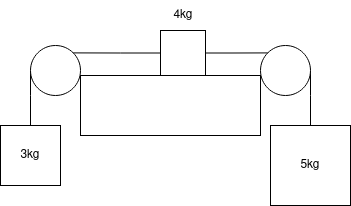
Assume that the system is just static and that the ropes and pulleys are smooth and light.
- What is the tension in the ropes?
- What is the direction and magnitude of the force of friction on the block on the table?
- Assume now the system has started to move. The coefficient of kinetic friction is 0.3. What is the acceleration of the block on the table?
Solution
1) The tension in the left rope is \(T_L = 3g\), and in the right rope is \(T_R = 5g\). Be very careful, on the horizontal part these forces are pointing in opposite directions!
2) Let's make the left direction positive. Since the block is not moving, then the forces are balanced, so
\[T_L + T_R + F_f = 0\]
Now, which way will friction point? I think it's easy to see that friction must resist the direction of motion, and if there was no friction, this block would move to the right (that is the direction of the heavier block). So friction points to the left.
\[3g - 5g + F_f = 0\]
\[F_f = 2g\]
3) Now the block is moving and we need to find the acceleration, so we need to use
\[F = ma\]
To find that resultant force, we need to find the force of friction. Since the block is still not moving vertically, we can say that the normal force is
\[N = 4g\]
And we know the coefficient of friction already
\[F_f = 0.3 \cdot 4g = 1.2g\]
The resultant force is given by
\[3g + 1.2g - 5g = F = -0.8g\]
And using the equation
\[-\frac{0.8 \cdot 9.81}{4} = -1.96ms^{-2}\]
Which is to the right, as we expect