Rotation

\( \newcommand{\colvec}[1]{\begin{pmatrix}#1\end{pmatrix}} \)

Many students struggle with rotation in physics, but the concepts are actually quite simple. I hope to describe them to you in a helpful way in this article.

Consider some vector \(\mathbf{r}(t)\). Its magnitude does not change but its direction does change, and varies with time. For a uniformly rotating vector we can define an angular frequency \(\omega\) which is the radians swept per unit time.

\[\omega = \frac{2 \pi}{T} = 2 \pi f\]

where \(T\) is the time for one full rotation (called the period) and \(f\) is the frequency, or number of full rotations per second. The \(2 \pi\) arises from the fact that there are \(2 \pi\) radians in a circle. Therefore, the angle swept by \(\mathbf{r}(t)\) in time \(t\) is \(\omega t \).

Now, consider how fast the rotating vector has to be going. Since it has to track out one rotation in time \(T\), and the distance that has to be traversed is \(2 \pi r\) (the circumference is \(2 \pi) times the radius), then the speed is given by

\[v = \frac{2 \pi r}{T} = \omega r \]

Now consider this velocity itself. We have the magnitude for constant \(\omega\), but velocity is also itself a vector. \(\mathbf{v}(t)\) is also a rotating vector. It always forms a tangent to the arc of rotation. This makes sense - if the object suddenly stops rotating would shoot out in a straight line tangent to the current arc. Think about hammer throwers in the olympics - they rotate rapidly on the spot and when they let go of the hammer it flies out straight over the field rather than continue in a circle.

If \(\omega\) is constant, then \(v\) will also be constant. Consider a sort of unusual concept but think about the "position" of the velocity vector in velocity space. In velocity space, one rotation will mean that \(\mathbf{v}(t)\) traces out a circle of circumference \(2 \pi v\). What causes \(\mathbf{v}(t)\) to change direction?

Some acceleration, of course. Consider the same analysis we just did with velocity. We now have to track out a "distance" \(2 \pi v\) in time \(T\).

\[a = \frac{2 \pi v}{T} = \omega v = \omega^2 r\]

Consider the hammer thrower again. The acceleration is provided by the hammer thrower - and that acceleration is always towards the hammer thrower. This is again a tangent, but this time to the velocity vector. We can see that the acceleration vector for rotation is given by

\[\mathbf{a}(t) = -\omega^2 \mathbf{r}(t)\]

The negative sign is there because it points in the opposite direction to \(\mathbf{r}(t)\).

Let's introduce the concept of reference frames that rotate with respect to one another. The following diagram shows two reference frames that have a rotation around the z axis. In other words, they have the same z axis but x and y are rotated with respect to one another.

If you consider the geometry, then it's quite easy to show the following results

\[a = x \cos(\theta), b = y \sin(\theta), c = y \cos(\theta), d = x \sin(\theta)\]

Therefore, we can write

\[x^\prime = a + b, y^\prime = c - d\]

Substituting we find

\[x^\prime = x \cos(\theta) + y \sin(\theta)\]

\[y^\prime = -x \sin(\theta) + y \cos(\theta)\]

What is really useful in rotating reference frames is a rotation matrix. Therefore, in matrix form we would write

\[\colvec{x^\prime\\y^\prime\\z^\prime} = \begin{pmatrix} \cos(\theta) & \sin(\theta) & 0\\ -\sin(\theta) & \cos(\theta) & 0\\ 0 & 0 & 1 \end{pmatrix} \colvec{x\\y\\z} \]

That allows us to convert between reference frames that are statically rotated with respect to one another. Now let us also consider if they are continually rotating with time. First, define some rotation matricies.

\[\colvec{x\\y\\z} = \begin{pmatrix} \cos(\omega t) & -\sin(\omega t) & 0\\ \sin(\omega t) & \cos(\omega t) & 0\\ 0 & 0 & 1 \end{pmatrix} \colvec{x^\prime\\y^\prime\\z^\prime} \]

Which is just the transpose of the rotation matrix we derived. If you have a rotation matrix \(C\) that rotates from \(A\) to \(B\) then the rotation matrix from \(B\) to \(A\) is \(C^T\). Rotation matricies are also always orthogonal, meaning the transpose is the same as the inverse i.e. \(C^T = C^{-1}\). The other difference of course being we have replaced \(\theta\) with \(\omega t\).

Let's try differentiating this matrix. We will need to recall the product rule for differentiation which is

\[f(x) = u(x) v(x)\]

\[\dot{f}(x) = \dot{u}(x) v(x) + u(x) \dot{v}(x)\]

To differentiate it is easier to expand out of the matrix form and then repackage it at the end, so

\[x = x^\prime \cos(\omega t) - y^\prime \sin(\omega t)\]

\[y = x^\prime \sin(\omega t) + y^\prime \cos(\omega t)\]

\[ \frac{dx}{dt} = \dot{x^\prime} \cos(\omega t) - x^\prime \omega \sin(\omega t) - \dot{y^\prime} \sin(\omega t) - y^\prime \omega \cos(\omega t) \]

\[ \frac{dy}{dt} = \dot{x^\prime} \sin(\omega t) + x^\prime \omega \cos(\omega t) + \dot{y^\prime} \cos(\omega t) - y^\prime \omega \sin(\omega t) \]

I won't explicitly do \(z\) since it is trivial

Collecting like terms into matrix form we get

\[ \frac{d}{dt} \colvec{x\\y\\z} = \begin{pmatrix} -\sin(\omega t) & -\cos(\omega t) & 0\\ \cos(\omega t) & -\sin(\omega t) & 0\\ 0 & 0 & 1 \end{pmatrix} \colvec{x^\prime\\y^\prime\\z^\prime} + \begin{pmatrix} \cos(\omega t) & -\sin(\omega t) & 0\\ \sin(\omega t) & \cos(\omega t) & 0\\ 0 & 0 & 1 \end{pmatrix} \colvec{\dot{x^\prime}\\\dot{y^\prime}\\\dot{z^\prime}} \]

The second term is the velocity vector in the primed coordinate frame as seen from the unprimed coordinate frame. The first term has some interesting properties though. Let's explore those.

\[\mathbf{\omega} = \omega \mathbf{\hat{z}}, \mathbf{r} = x \mathbf{\hat{x}} + y \mathbf{\hat{y}} + z \mathbf{\hat{z}}\]

\(\mathbf{\omega}\) is called the angular velocity, which in This case is the rate of rotation about the z axis.

Consider now the cross product of them both

\[\mathbf{\omega} \times \mathbf{r} = \omega \mathbf{\hat{z}} \times (\mathbf{\hat{x}} + y \mathbf{\hat{y}} + z \mathbf{\hat{z}}) = -\omega y \mathbf{\hat{x}} + \omega x \mathbf{\hat{y}} \]

Written in matrix form this would be

\[\mathbf{\omega} \times \mathbf{r} = \omega \colvec{-y\\x\\0}\]

Let's look at the first term again, and see if we can't make it match this result. In other words, let's try and prove that

\[ \omega \begin{pmatrix} -\sin(\omega t) & -\cos(\omega t) & 0\\ \cos(\omega t) & -\sin(\omega t) & 0\\ 0 & 0 & 1 \end{pmatrix} \colvec{x^\prime\\y^\prime\\z^\prime} = \omega \colvec{-y\\x\\0} \]

Let's write this out in the non-matrix form, again I will ignore the trivial z component

\[-x^\prime \sin(\omega t) - y^\prime \cos(\omega t) = -y\]

\[x^\prime \cos(\omega t) - y^\prime \sin(\omega t) = x\]

And now if we refer back to the original definition of this rotating reference frame and expand it we find

\[x = x^\prime \cos(\omega t) - y^\prime \sin(\omega t)\]

\[y = x^\prime \sin(\omega t) + y^\prime \cos(\omega t)\]

Which are a match, so we have proven it. Now using all of these results we can see that

\[\frac{d_a \mathbf{r}}{dt} = \frac{d_r \mathbf{r}}{dt} + \mathbf{\omega} \times \mathbf{r}\]

where \(\frac{d_a \mathbf{r}}{dt}\) is the velocity of some point in the unprimed reference frame and \(\frac{d_r \mathbf{r}}{dt}\) is the velocity of the same point in the primed reference frame.

This is a very important result, and helps answer a question I struggled with during my undergraduate degree. Let's make a point rotate with the primed velocity frame, such that it's velocity in that frame is 0, we would have

\[\frac{d_a \mathbf{r}}{dt} = \mathbf{\omega} \times \mathbf{r}\]

Which way, then, should \(\mathbf{\omega}\) point? Imagine a clock on the wall, where the tip of the minute hand is the point we are considering in the rotating reference frame. Should \(\mathbf{\omega}\) point to 6 o'clock or 5 o'clock? All of the radial directions are totally not helpful because the hand usually doesn't point to any of them (although it will point at one of them). The only way to define this is perpendicular - in this case going into the clock to keep a right hand rule. I always wondered what was "pointing" perpendicular to the rotation when it came to angular velocity.

The velocity of a rotating point can be described as

\[\omega r \sin(\theta) = v\]

dealing with only the magnitudes, but in a more useful vector form we might write

\[|\mathbf{\omega}| |\mathbf{r}| \sin(\theta) \mathbf{\hat{n}} = \mathbf{v}\]

Where this \(\mathbf{\hat{n}}\) is a vector pointing in the direction of \(\mathbf{v}\) which is itself perpendicular to the plane made by \(\mathbf{\omega}\) and \(\mathbf{r}\). In other words

\[\mathbf{\omega} \times \mathbf{r} = |\mathbf{\omega}| |\mathbf{r}| \sin(\theta) \mathbf{\hat{n}} = \mathbf{v}\]

Let's now turn our attention to acceleration vectors in rotating frames. Just a reminder, the relationship between a velocity vector in one frame to another when the frames are rotated with respect to one another (but not rotating) is given by

\[ \colvec{\dot{x}\\\dot{y}\\\dot{z}} = \begin{pmatrix} \cos(\theta) & -\sin(\theta) & 0\\ \sin(\theta) & \cos(\theta) & 0\\ 0 & 0 & 1 \end{pmatrix} \colvec{\dot{x}^\prime\\\dot{y}^\prime\\\dot{z}^\prime} \]

This carries obvious parallels with the transformation that we have already differentiated. Therefore, we can think of differentiating a vector in a rotated reference frame as applying the following operation

\[\frac{d_a}{dt} = \frac{d_r}{dt} + \mathbf{\omega} \times\]

So applied to vector \(\mathbf{K}\)

\[\frac{d_a \mathbf{K}}{dt} = \frac{d_r \mathbf{K}}{dt} + \mathbf{\omega} \times \mathbf{K}\]

So applying this to a velocity vector \(\mathbf{v}\)

\[\frac{d_a \mathbf{v}}{dt} = \frac{d_r \mathbf{v}}{dt} + \mathbf{\omega} \times \mathbf{v}\]

But we have already have an alternative expression for \(\mathbf{v}\)

\[\mathbf{v} = \frac{d_a \mathbf{r}}{dt} = \frac{d_r \mathbf{r}}{dt} + \mathbf{\omega} \times \mathbf{r}\]

Therefore, we can derive

\[\frac{d_a \mathbf{v}}{dt} = \frac{d_r}{dt} \left( \frac{d_r}{dt} \mathbf{r} + \mathbf{\omega} \times \mathbf{r} \right) + \mathbf{\omega} \times \left(\frac{d_r}{dt} \mathbf{r} + \mathbf{\omega} \times \mathbf{r} \right) \]

Getting this into a more useful form will require the use of some vector relationships. The first is

\[\frac{d}{dx}(\mathbf{A} \times \mathbf{B}) = \frac{d \mathbf{A}}{dx} \times \mathbf{B} + \mathbf{A} \times \frac{d \mathbf{B}}{dx} \]

Which allows us to rearrange the expression into

\[\frac{d_a}{dt} \mathbf{v} = \frac{d_r^2 \mathbf{r}}{dt^2} + \frac{d_r \mathbf{\omega}}{dt} \times \mathbf{r} + 2 \mathbf{\omega} \times \frac{d_r \mathbf{r}}{dt} + \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r})\]

We can also rewrite the last part of this expression like this

\[\mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r}) = (\mathbf{\omega} \cdot \mathbf{r}) \mathbf{\omega} - (\mathbf{\omega} \cdot \mathbf{\omega}) \mathbf{r} \]

Let's consider now some astronauts living in space. They live in a space station that has "artificial gravity" due to its rotation. The coordinate system attached to this space station is the primed reference frame. The rate of rotation is not changing, so \(\frac{d_r \mathbf{\omega}}{dt} = 0\), therefore in this circumstance our expression becomes

\[\frac{d_a}{dt} \mathbf{v} = \frac{d_r^2 \mathbf{r}}{dt^2} + 2 \mathbf{\omega} \times \frac{d_r \mathbf{r}}{dt} + \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r})\]

If we rearrange for the acceleration we find

\[\frac{d_r^2 \mathbf{r}}{dt^2} = \frac{d_a \mathbf{v}}{dt} - 2 \mathbf{\omega} \times \frac{d_r \mathbf{r}}{dt} - \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r}) \]

The astronaut is in equilibrium and static in the primed reference frame, therefore \(\frac{d_r \mathbf{r}}{dt} = 0\) and he experiences no resultant force.

\[0 = \mathbf{F} - m \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r})\]

We can see that \(\mathbf{F}\) must be directed towards the earth which is the centripetal force in the unprimed frame. The force \(- m \mathbf{\omega} \times (\mathbf{\omega} \times \mathbf{r})\) is the centrifugal force. The centrifugal force is sometimes said to "not exist" but that is only true in the unprimed reference frame. This force is very real to the astronaut in the primed reference frame.

Kepler Laws

We will now take a look at the Kepler laws of motion. These laws describe, but don't explain, the motion of planets. Kepler was working with the precise measurements of objects in the solar system taken by Brahe, and wanted to fit them to some equation. At the time it was assumed that the planets orbited in perfect circles (it was, incidentally, also thought that planets were perfect spheres), but Kepler found that the data collected by Brahe couldn't fit circular orbits. Rather than assuming the data was wrong, Kepler assumed the orbits could fit some other shape than a circle - and eventually he found excellent agreement between the data and elliptical orbits.

Kepler "derived" the first law of elliptical orbits from data matching i.e. an empirical model. We shall look at the first law in light of Newton's later laws of gravitation, and observe some properties. Then you will derive the second and third laws.

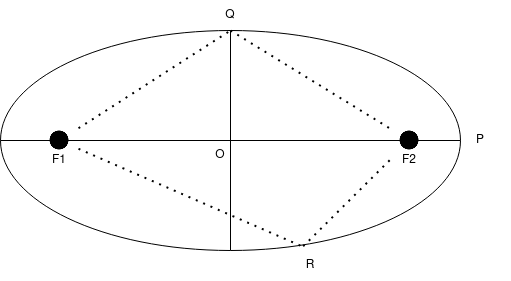
First, look at the above ellipse. The origin is \(O\), the centre of the ellipse. \(F_1\) and \(F_2\) are the two focal points. The line \(OP\) is the semi-major axis and usually given the letter \(a\). The line \(OQ\) is the semi-minor axis and given the letter \(b\). The line \(F_1 R F_2\) is always the same length, no matter where \(R\) is on the perimeter of the ellipse, and has total length \(2a\). The length from each of the focal points to the centre is the same, and often represented as a fraction of the semi-major axis i.e. \(F_1 O = F_2 O = ea\). This \(e\) is the eccentricity. An eccentricity of 1 is a perfect circle. Lower eccentricites are more extreme ellipses. The semi-major and semi-minor axis are related by the expression

\[a = \frac{b}{\sqrt{1-e^2}}\]

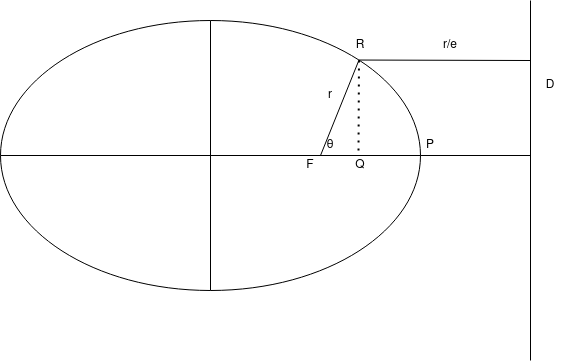
Take a look at the above ellipse. We call the distance from \(F\) to line \(D\), \(d\). We can see that \(d = r \cos(\theta) + r/e\). This gives us an equation for \(r\) as it depends on \(\theta\)

\[r(\theta) = \frac{ed}{1+ e \cos(\theta)}\]

We've already introduced the idea of a gravitational field in the past. The field vector is given by

\[\mathbf{g} = -G \frac{m}{r^3} \mathbf{r}\]

Consider a gravitational field produced by mass \(m_1\). We now place \(m_2\) inside that field. The force experienced by \(m_2\) caused by \(m_1\) is given by

\[\mathbf{W} = m_2 \mathbf{g_1} = -G \frac{m_2 m_1}{r^3} \mathbf{r}\]

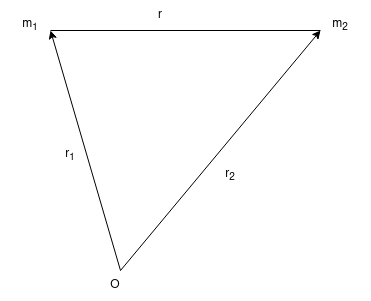
Consider what is meant by \(\mathbf{r}\). If we look at the above diagram, we can see that \(r = r_2 - r_1\). This is important so that we can get our minus signs in the right places. Therefore,

\[\mathbf{W}_1 = G \frac{m_1 m_2}{r^3} \mathbf{r}\]

\[\mathbf{W}_2 = -G \frac{m_1 m_2}{r^3} \mathbf{r}\]

Where \(\mathbf{W}_1\) is the wight of \(m_1\) in the field of \(m_2\), and vice versa.

Since these weights are resultant forces, we can also use Newton's second law to give us

\[m_1 \frac{d^2}{dt^2} \mathbf{r}_1 = \mathbf{W}_1 = G \frac{m_1 m_2}{r^3} \mathbf{r}\]

\[m_2 \frac{d^2}{dt^2} \mathbf{r}_2 = \mathbf{W}_2 = -G \frac{m_1 m_2}{r^3} \mathbf{r}\]

These two expressions sum to 0, so

\[m_1 \frac{d^2}{dt^2} \mathbf{r}_1 + m_2 \frac{d^2}{dt^2} \mathbf{r}_2 = 0\]

Now we want to integrate this to give us the following expressions

\[m_1 \frac{d}{dt} \mathbf{r}_1 + m_2 \frac{d}{dt} \mathbf{r}_2 = \mathbf{p}\]

\[m_1 \mathbf{r}_1 + m_2 \mathbf{r}_2 = \mathbf{p} t + \mathbf{q}\]

Where \(\mathbf{p}\) is a constant momentum vector and \(\mathbf{q}\) is some constant displacement vector.

If we subtract \(\frac{d^2}{dt^2} \mathbf{r}_1\) from \(\frac{d^2}{dt^2} \mathbf{r}_2\), we arrive at

\[\frac{d^2}{dt^2} \mathbf{r} = -G \frac{(m_1 + m_2)}{r^3} \mathbf{r}\]

Now we can observe some properties of this equation. For shorthand let's call the acceleration \(\mathbf{a}\) and velocity \(\mathbf{v}\) such that

\[\frac{d^2}{dt^2} \mathbf{r} = \mathbf{a}\]

\[\frac{d}{dt} \mathbf{r} = \mathbf{v}\]

Then

\[\mathbf{r} \times \mathbf{a} = -G \frac{m_1 + m_2}{r^3} \mathbf{r} \times \mathbf{r} = 0\]

We can also write

\[\frac{d}{dt} (\mathbf{r} \times \mathbf{v}) = 0\]

Which shows that

\[\mathbf{r} \times \mathbf{v} = \text{some constant vector}\]

We call this conserved quantity \(\mathbf{h}\), and it will be essential for you when you derive the second and third Kepler laws

Now consider the scalar product

\[\mathbf{v} \cdot \mathbf{a} = -G \frac{m_1 + m_2}{r^3} \mathbf{v} \cdot \mathbf{r}\]

The left hand side might be familiar to you from product rule work, but if not then

\[ \frac{d}{dt} \frac{v^2}{2} = \frac{1}{2} \frac{d}{dt} \mathbf{v} \cdot \mathbf{v} + \frac{1}{2} \mathbf{v} \cdot \frac{d}{dt} \mathbf{v} = \mathbf{v} \cdot \mathbf{a} \]

The right hand side can also be manipulated, but it is more complex

\[ \frac{d}{dt} \left( \frac{G (m_1 + m_2)}{r} \right) = \frac{d}{dt} \left( \frac{G(m_1 + m_2)}{\sqrt{x^2 + y^2 + z^2}} \right) \]

Since \(r = \sqrt{x^2 + y^2 + z^2}\)

\[ \frac{d}{dt} \left( \frac{G(m_1 + m_2)}{\sqrt{x^2 + y^2 + z^2}} \right) = G (m_1 + m_2) \left( \frac{1}{2} \frac{1}{(x^2 + y^2 + z^2)^{\frac{3}{2}}} 2x \frac{dx}{dt} + \dots \right) \]

Where the extra expressions for each of the three dimensions of space are omitted, but the same logic applies. We can simplify all of this by

\[ \frac{d}{dt} \left( \frac{G(m_1 + m_2)}{\sqrt{x^2 + y^2 + z^2}} \right) = - \frac{G (m_1 + m_2)}{r^3} \left( x \frac{dx}{dt} + y \frac{dy}{dt} + z \frac{dz}{dt} \right) = - \frac{G (m_1 + m_2)}{r^3} \mathbf{r} \cdot \mathbf{v} \]

So, we can write

\[\frac{d}{dt} \left( \frac{v^2}{2} - \frac{G(m_1 + m_2)}{r} \right) = 0\]

And we have yet another conserved quantity

Finally, let's take the vector product of \(\mathbf{a}\) with \(\mathbf{h}\). First,

\[ \mathbf{h} = \mathbf{r} \times \mathbf{v} = \mathbf{r} \times \left( \frac{d_r}{dt} \mathbf{r} + \mathbf{\omega} \times \mathbf{r} \right) = \mathbf{r} \times \left( \frac{dr}{dt} \hat{\mathbf{x}}^\prime + \omega r \hat{\mathbf{y}}^\prime \right) = \omega r^2 \hat{\mathbf{z}} \]

Where we now align the rotating \(x^\prime\) axis with \(\mathbf{r}\), with the x and y axis perpendicular but in the same plane. So,

\[ \mathbf{a} \times \mathbf{h} = -G \frac{m_1 + m_2}{r^3} \mathbf{r} \times \omega r^2 \hat{\mathbf{z}} = -G \frac{m_1 + m_2}{r^3} r^3 \omega \hat{\mathbf{x}}^\prime \times \hat{\mathbf{z}} \]

Which becomes

\[\mathbf{a} \times \mathbf{h} = G(m_1 + m_2) \omega \hat{\mathbf{y}}^\prime\]

But

\[\omega \hat{\mathbf{y}}^\prime = \frac{d \hat{\mathbf{x}}^\prime}{dt}\]

So, rewriting our expression as a time derivative

\[ \frac{d}{dt} (\mathbf{v} \times \mathbf{h}) = \frac{d}{dt} (G (m_1 + m_2) \hat{\mathbf{x}}^\prime) \]

So,

\[ \mathbf{v} \times \mathbf{h} - G (m_1 + m_2) \hat{\mathbf{x}}^\prime = \text{some constant vector} \]

So, taking the integral, we see

\[ \mathbf{v} \times \mathbf{h} = G(m_1 + m_2) (\hat{\mathbf{x}}^\prime + \mathbf{e}) \]

Where \(\mathbf{e}\) is a vector whose magnitude determines the kind of orbit we are dealing with. 0 for a circular orbit, above 0 and below one for an elliptical orbit, 1 for a parabolic orbit and above 1 for a hyperbolic orbit.

In other words, this whole derivation was to arrive back at the eccentricity of an orbit!

So, the final thing to do is

\[ \mathbf{r} \cdot (\mathbf{v} \times \mathbf{h}) = G(m_1 + m_2)(r + er \cos(\theta)) \]

Where \(\theta\) is the angle between \(\mathbf{r}\) and \(\mathbf{e}\)

Since

\[ \mathbf{r} \cdot (\mathbf{v} \times \mathbf{h}) = (\mathbf{r} \times \mathbf{v}) \cdot \mathbf{h} = \mathbf{h} \cdot \mathbf{h} = h^2 \]

Then

\[ r(\theta) = \frac{h^2 / G(m_1 + m_2)}{(1 + e \cos(\theta))} \]

Workshop: Kepler's Second Law

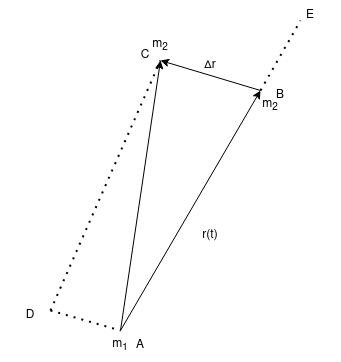
Consider the above image. \(m_2\) starts at \(B\) but orbits to \(C\). The vector product \(\mathbf{r} \times \Delta \mathbf{r}\) is

\[ |\mathbf{r}| |\Delta \mathbf{r} | \sin(\phi) \hat{\mathbf{z}} \]

Where \(\phi\) is the angle made by \(CBE\)

a) show that \(r \Delta r \sin(\phi)\) is the area of the parallelogram \(ABCD\)

b) Hence, show that the area swept, \(\Delta \mathbf{A}\) by \(\mathbf{r}\) in time \(\Delta t\) is

\[\Delta \mathbf{A} = \frac{1}{2} \mathbf{r} \times \Delta \mathbf{r}\]

c) Hence show that

\[\frac{d}{dt} \mathbf{A} = \frac{1}{2} h \hat{z}\]

Workshop: Kepler's Third Law

We now want to derive Kepler's third law

a) Show that

\[ \frac{\pi a b}{T} = \frac{1}{2} \sqrt{p G(m_1 + m_2)} \]

Where

\[p = a (1 - e^2)\]

And remember that the area of a circle or ellipse is given by \(A = \pi a b\)

b) Show that

\[ T^2 = \frac{4 \pi^2}{G(m_1 + m_2)} a^3 \]